| Главная » Статьи » Студентам » Логистика |
|
Чтобы проиллюстрировать марковские процессы рассмотрим задачу, в которой состояниями является бренды, а вероятности переходов соответствуют вероятностям изменения предпочтения одного бренда в пользу другого. Предположим, что для решения данной задачи было опрошено 1000 респондентов, а количество исследуемых брендов равно 4: А, В, С и D. На изменение предпочтений потребителей, то есть на переход к приобретению иного бренда, влияют реклама, цена, другие методы продвижения, качество, недовольство некоторыми параметрами. В табл. 1 представлены изменения количества потребителей по каждому бренду за месяц.
Табл. 1. Изменения количества
потребителей по каждой торговой марке за 1 месяц 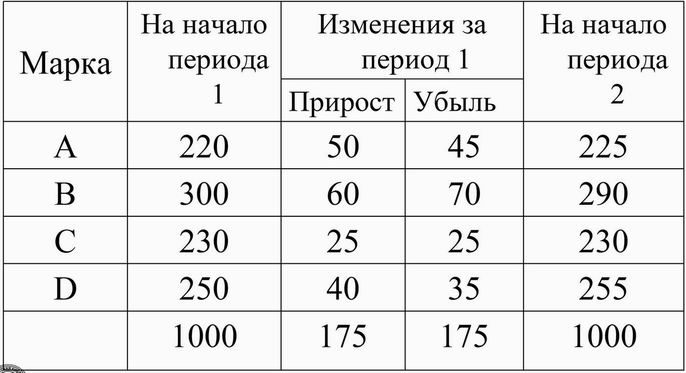 Исследуем торговую марку А. Изменение его потребителей за месяц равняется пяти (50-45). Однако, пользуясь приведенной выше таблицей, мы не можем определить структуру перешедших в группу потребителей марки А, то есть установить абсолютное или относительное значение увеличения потребителей А за счет перехода некоторых потребителей из группы В, из группы С, и, наконец, – D. Аналогично, не видно, сколько из группы А перешло в группу В, и так далее. Прежде чем, приступить к исследованию переходов, следует определить величины постоянной части потребителей, то есть тех, кто не изменяет своим предпочтениям и продолжает в последующем периоде приобретать тот вид продукции, который приобретал ранее. Для такого рода потребителей необходимо отыскать вероятности переходов из состояния в состояние для четырех марок. Экономическая интерпретация этих вероятностей выглядит следующим образом. Они соответствуют вероятности того, что предприятие сможет вернуть утраченных покупателей конкретной торговой марки. В нашем примере марка А утратил 45 покупателей, сохранив при этом 175 (220 – 45). Вероятность того, что количество покупателей марки А сохранится составляет 0,796 (175/220). Вероятности переходов для B, C и D соответственно составляют 0.767, 0.891 и 0.86. Анализируя тех покупателей, которые переключаются с одной торговой марки на другую, необходимо показать, как происходят данные изменения, чтобы построить матрицу вероятностей переходов. Такие данные требуют аккуратного сбора статистической информации (табл. 2). Можно исследовать не только чистые приросты или потери в разрезе одной торговой марки, но также взаимосвязи между марками. Например, в приросте потребителей марки А большая часть принадлежит потребителям марки В, хотя в тоже время большинство из потребителей марки А переключились на покупку марки В. Нули на главной диагонали означают отсутствие переходов внутри группы. Табл. 2. Детализация переходов потребителей от
одной торговой марки к другой за 1 месяц. 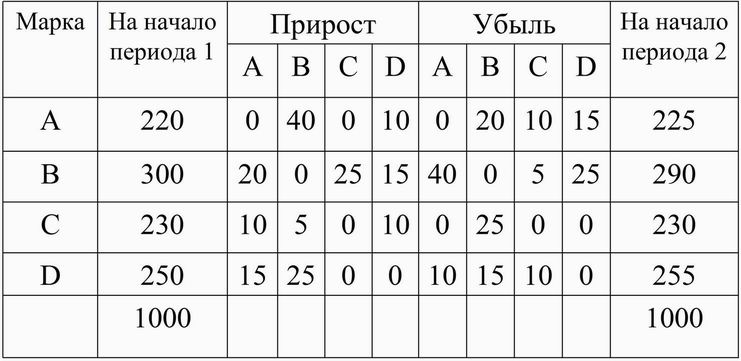 Следующим шагом является преобразование переходов
потребителей таким образом, чтобы все приросты и потери приняли вид
вероятностей переходов. Это изображено на рис. 1, где стрелки, ведущие к торговой
марке, обозначают положительный поток потребителей, а стрелки, нарисованные от торговой
марки, представляют отрицательный поток потребителей. Однако наиболее удобной
формой математических вычислений является все же матрица вероятностей переходов
(табл. 3).
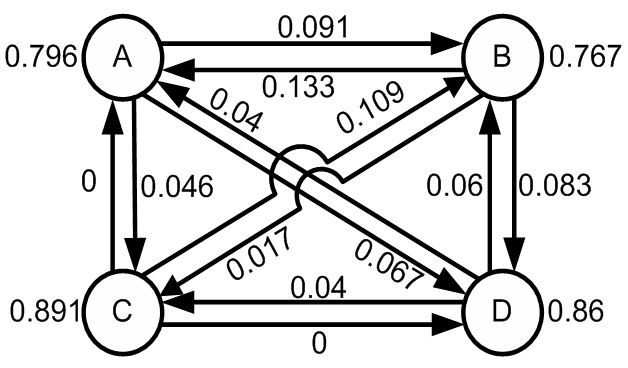 Рис. 1. Вероятности переходов потребителей между торговыми марками 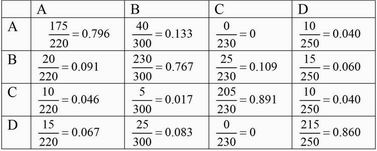 Табл. 3
Матрица вероятностей переходов 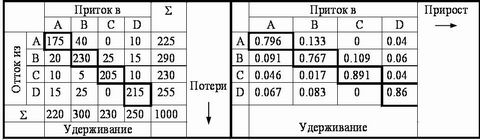 Строки матрицы вероятностей переходов отображают положительный поток потребителей для торговых марок, а столбцы – отрицательный поток. В табл. 3 первая матрица представлена в натуральных числах, тогда как вторая матрица – в виде вероятностей переходов. Надо напомнить, что эти вероятности применимы ко всем потребителям, поскольку рассчитываются на основе выборки в 1000 потребителей.
В первой строке первый элемент показывает вероятность того, что А сохранит своих покупателей, второй элемент показывает вероятность притока покупателей из группы В и т.д. В первом столбце первый элемент не теряет своей интерпретации, тогда как второй элемент показывает вероятность оттока потребителей группы А в группу потребителей В. Последующие элементы определяются по аналогии со вторым. Основным предположением является то, что потребители переходят на другую торговую марку не случайно. Покупки продукции в будущем зависят от выбора сделанного в прошлом. Марковские процессы могут быть
разного порядка. Марковские процессы первого порядка могут быть применены для
нахождения вероятностей выборов торговых марок в следующем периоде на основе
совершенных выборов марок в текущем периоде. Анализ второго порядка предполагает
выборы конкретной торговой марки в предстоящем периоде в зависимости от выборов
марок на два периода раньше, то есть происходивших в предшествующем текущему
периоду. Аналогично марковские процессы третьего порядка основываются на
потребительских предпочтениях на три периода раньше от предстоящего периода. Установлено, что рыночные доли A, B, C и D составляют 22, 30, 23 и 25 соответственно. Для предприятия представляется важным определение рыночных долей в следующем периоде. Для вычисления вероятных рыночных долей в периоде 2 следует матрицу вероятностей переходов умножить на столбец рыночных долей в периоде 1: 
Вероятные рыночные доли торговых
марок в периоде 3 могут вычисляться двумя способами. Первый является
продолжением только что проиллюстрированного метода – произведение исходной
матрицы вероятностей переходов на рыночные доли торговых марок в периоде 2. Второй метод заключается в возведении матрицы вероятностей перехода в квадрат до тех пор пока не будет достигнут нужный номер периода. После этого полученная матрица умножается на исходные рыночные доли. Рассмотри первый метод. 
Преимуществом данного метода является возможность исследовать изменения рыночных долей от периода к периоду. Результат, полученный вторым методом совпадает с результатом первого метода: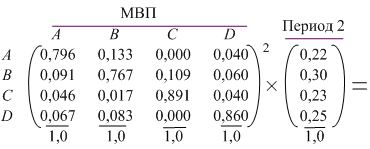  Дадим интерпретацию квадратичной матрицы на примере расчета первого элемента.    
Доля возвращенных покупателей торговой марки А в общем количестве рассчитывается как сумма приведенных выше показателей:
Приведенный выше анализ цепей Маркова не превосходит первый порядок поскольку вероятность наступления будущего события зависит исключительно от результатов некоторого периода в прошлом. В марковских процессах высшего порядка предсказание будущего события зависит от непосредственно предшествующего ему события. Нестабильность потребительских предпочтений приводит к увеличению порядка марковского процесса. | |
| Категория: Логистика | Добавил: kvn2us (20.04.2009) | | |
| Просмотров: 2975 | |