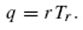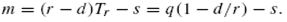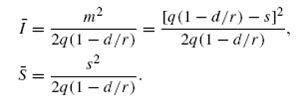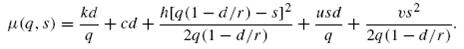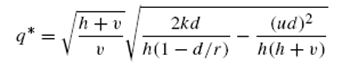| Главная » Статьи » Студентам » Логистика |
d – постоянная
интенсивность потребления материала; T – период между двумя
последовательными заказами; q – размер заказа;
c – стоимость покупки
материала (независимо от размера закупки);
k – фиксированные
затраты на осуществление заказа; h – затраты на
хранение; u – потери вследствие
дефицита материала, независимо от периода и объема дефицита;
v – удельные затраты
вследствие дефицита материала.
Требуемое количество материала определяется, исходя из соотношения
Затраты на хранение пропорциональны стоимости покупки материала:
Параметр p – это процентная ставка. Пусть I(t) – объем запасов в момент времени t, m – максимальный объем запасов, s – максимально допустимый размер дефицита, tl – длительность поставки, т.е. промежуток времени от момента заказа до момента получения материала. Задача заключается в определении q (и T) и s, при которых общие затраты минимальны. Динамика уровня запасов схематично представлена на рис. 1
Рис. 1. Динамика уровня запасов Время восполнения запасов обозначим через
Максимальный уровень запаса m задается уравнением: 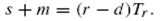 Тогда используя два предыдущих уравнения, получим
Средние совокупные затраты в единицу времени составят: Затраты на хранение и потери от недостаточного количества материала зависят от среднего уровня запасов и среднего уровня дефицита, которые рассчитываются соответственно по формулам: 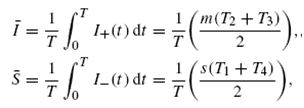 где 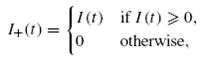 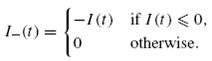 Поскольку 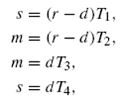 то 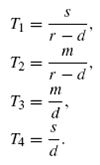 Следовательно Подставляя уравнения (2) и (3) в уравнение (1), получаем: Если дефицит допускается, то точка (q*, s*) вогнутой функции µ(q, s) находится путем решения системы уравнений частных производных:
В результате получаем
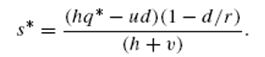 Если нехватка материала не допускается (s = 0), уравнение (4) принимает вид: 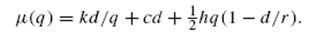 Решая уравнение 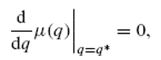 формула оптимального размера заказа примет вид 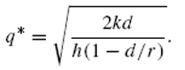 Функции величин затрат представлены на рис. 2 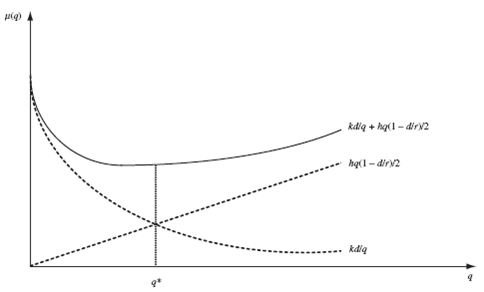 Рис. 2. Величины затрат, как функции от q | |
| Категория: Логистика | Добавил: kvn2us (05.06.2009) | | |
| Просмотров: 4075 | |

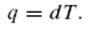
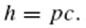
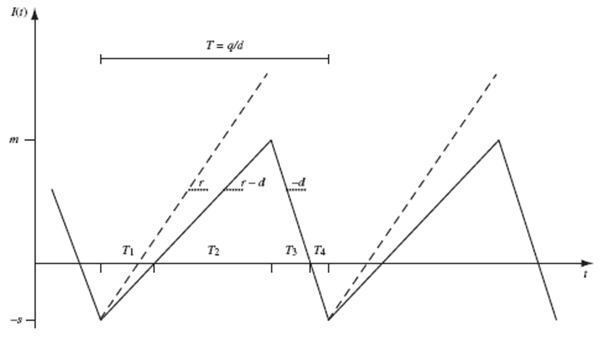
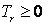 ,
,