| Главная » Статьи » Студентам » Имитационное моделирование |
Определение 4. Случайный процесс называется марковским, если для любого момента времени Каждому переходу из одного состояния в другое – соответствует вероятность Отметим, что в общем одношаговая матрица вероятностей
переходов, определяемая как Таким образом, марковская цепь может быть однородной, если вероятности переходов не зависят от номера шага, то есть Если вероятности переходов меняются от шага к шагу, марковская цепь называется неоднородной. Предположим, имеется конечная марковская цепь, в которой число различных состояний не превышает трех. Следовательно, МВП имеет вид 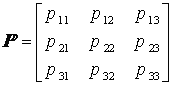 . .Тогда Пример 5.3.
Допустим, необходимо определить вероятность того, что через три дня установится
дождливая погода при условии, что сегодня облачно. Для этого необходимо
определить 2-й и 3-й элементы матрицы 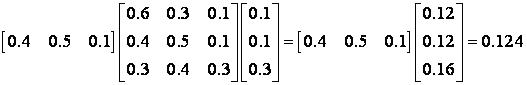 . .Заметим, что начальное
(конечное) состояние соответствует строке (столбцу) Если задана целая запись прошлых состояний (в понедельник – солнечно, вторник – солнечно, среда – облачно), то вычисление вероятности того, что в субботу пойдет дождь, будет происходить таким же способом, поскольку можем игнорировать информацию обо всех днях за исключением последнего. Пример 5.4. Модифицируем
задачу: необходимо определить, какой будет вероятность наступления дождливой
погоды в субботу и воскресенье. Чтобы ответить на этот вопрос, прежде обозначим
через Тогда получаем, что 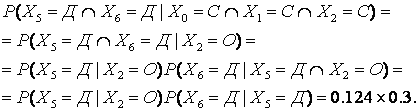 Заметим, что в данном уравнении использовались
обозначения Подытожим основное правило прогнозирования на основе прошлых данных: - для проведения расчетов используется только последняя запись о состоянии системы, а информация о ее прошлом не берется во внимание; - определяется вероятность перехода в конкретное состояние в следующий момент времени; - на основе этой информации определяется вероятность перехода в следующий прогнозируемый момент времени; - процедура продолжается до тех пор, пока не достигнем интересуемого момента времени; - эти вероятности перемножаются. Чтобы закрепить полученные навыки построения МВП, рассмотрим ситуацию, когда группа покупателей заходит в торговый павильон и попадает в первый отдел, из которого выйти можно только, перейдя в следующий отдел. Вход и выход из павильона блокируются (см. рис. 5.3). 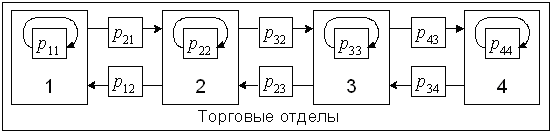
Рис. 5.3. Схема допустимых путей перемещения
покупателей Пусть
общее количество покупателей равно N и в определенный момент времени Предположим,
что в один из моментов времени известно, что из покупателей во втором отделе Тогда
введем 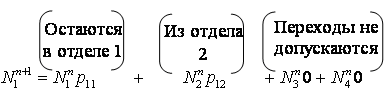  или в матричном виде При этом Если предположить, что покупатели не запоминают, в каком
отделе они уже были, то вероятности
Принимая величину Пусть торговый павильон имеет 5 отделов, и выход из него возможен только через пятый отдел (рис. 5.4). 
Рис. 5.4. Схема допустимых путей перемещения покупателей по торговому павильону с пятью отделами Тогда переходы из отдела в отдел описываются следующим уравнением 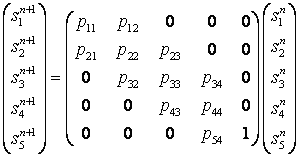 . .
Экономическим примером применения цепей Маркова может служить прогнозирование переходов клиентов от одного брэнда к другому на определенном рыночном сегменте или в розничном торговом предприятии. В данном случае в начальный момент времени известны объемы спроса на каждый брэнд и в результате опроса определены вероятности перехода от одного брэнда к другому. | |
| Категория: Имитационное моделирование | Добавил: kvn2us (27.01.2009) | | |
| Просмотров: 3970 | Комментарии: 1 |
