| Главная » Статьи » Студентам » Имитационное моделирование |
Критерий согласия Пирсона (Хи-квадрат) и критерий Колмогорова-СмирноваЗадание
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 2 | 3 | 4 | 6 | 4 | 3 | |
| 5 | 4 | 2 | 1 | 4 | 5 | 3 |
| 4 | 5 | 3 | 5 | 8 | 2 | 2 |
| 3 | 1 | 3 | 6 | 2 | 1 | 3 |
| 2 | 7 | 1 |
Приняв уровень значимости alpha=0.05, проверить согласие этих данных обычного месяца с распределением Пуассона, пользуясь критерием Хи-квадрат. Перепроверить данные с помощью критерия Колмогорова-Смирнова, по прежнему принимая alpha=0.05.
Методические указания
Широко используемыми на практике критериями проверки статистических гипотез выступают следующие:- критерий согласия Хи-квадрат
- критерий Крамера-фон Мизеса
- критерий Колмогорова-Смирнова
Критерий Хи-квадрат предпочтителен, когда исследуются большие объемы выборок. При малых объемах выборок этот критерий практически не пригоден.
Нулевая гипотеза при применении общих критериев согласия записывается в форме
Н0: Fn(x) = F(x),
где Fn(x) – эмпирическая функция распределения вероятностей; F(x) – гипотетическая функция распределения вероятностей.
Критерий Пирсона X2 основан на сравнении эмпирической гистограммы распределения случайной величины с ее теоретической плотностью. Диапазон изменения экспериментальных данных разбивается на k интервалов, и подсчитывается статистика:
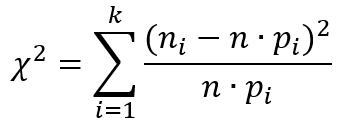
где ni – количество значений случайной величины, попавших в i-й интервал; n – объем выборки; F(x) – гипотетический теоретический закон распределения вероятностей случайной величины; pi = F(xi+1) — F(xi) – теоретическая вероятность попадания случайной величины в i-й интервал.
Статистика X2 имеет распределение Хи-квадрат с f = n — 1 степенями свободы в том случае, когда проверяется простая нулевая гипотеза H0, т.е., когда гипотетическое распределение, на соответствие которому проверяется эмпирический ряд данных, известно с точностью до значения своих параметров.
Правило проверки гипотезы:
если X2 > X2alpha(f)
то на уровне значимости alpha, т. е. с достоверностью (1 — alpha) гипотеза
H0 отклоняется.
На мощность статистического критерия X2 сильное влияние оказывает чиcло интервалов разбиения гистограммы (k) и порядок ее разбиения (т. е. выбор длин интервалов внутри диапазона изменения значений случайной величины). На практике принято считать, что статистику X2 можно использовать, когда npi >= 5.
Такое приближение допустимо и тогда, когда не более, чем в 20% интервалов имеет место 1 <= npi <= 5.
Одна из рекомендаций по расчету k сводится к вычислению:
k = 1+ 3,32·lg n
При n >= 200 можно выбирать k из условия
k = 4·{0,75·(n — 1)2}1/5 ≈ 3,78·(n — 1)2/5.
Еще одно простое правило: выбрать как можно большее k, но не превышающее n/5:
k <= n / 5
Критерий Крамера-фон Мизеса дает хорошие результаты при малых объемах выборок (менее 10). Однако вопрос о доверительной вероятности остается нерешенным (эта вероятность мала при значительных размерах доверительных интервалов.
Исходя из этого, полагают, что реальные объемы выборок, которые можно получить, находятся в диапазоне от 10 до 100.
Критерий Колмогорова-Смирнова также целесообразно использовать для выборки указанных объемов в тех случаях, когда проверяемое распределение непрерывно и известны среднее значение и дисперсия проверяемой совокупности.
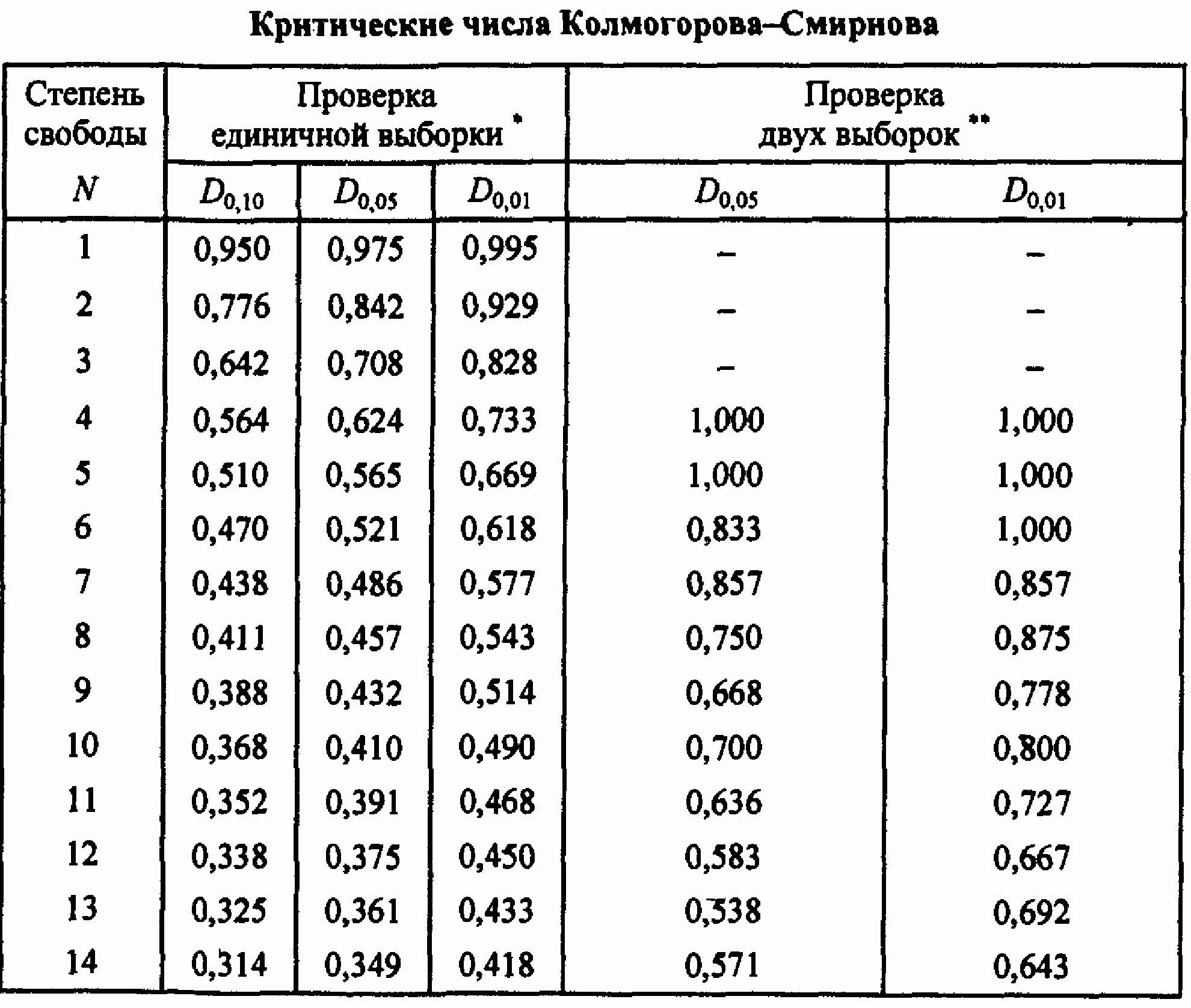
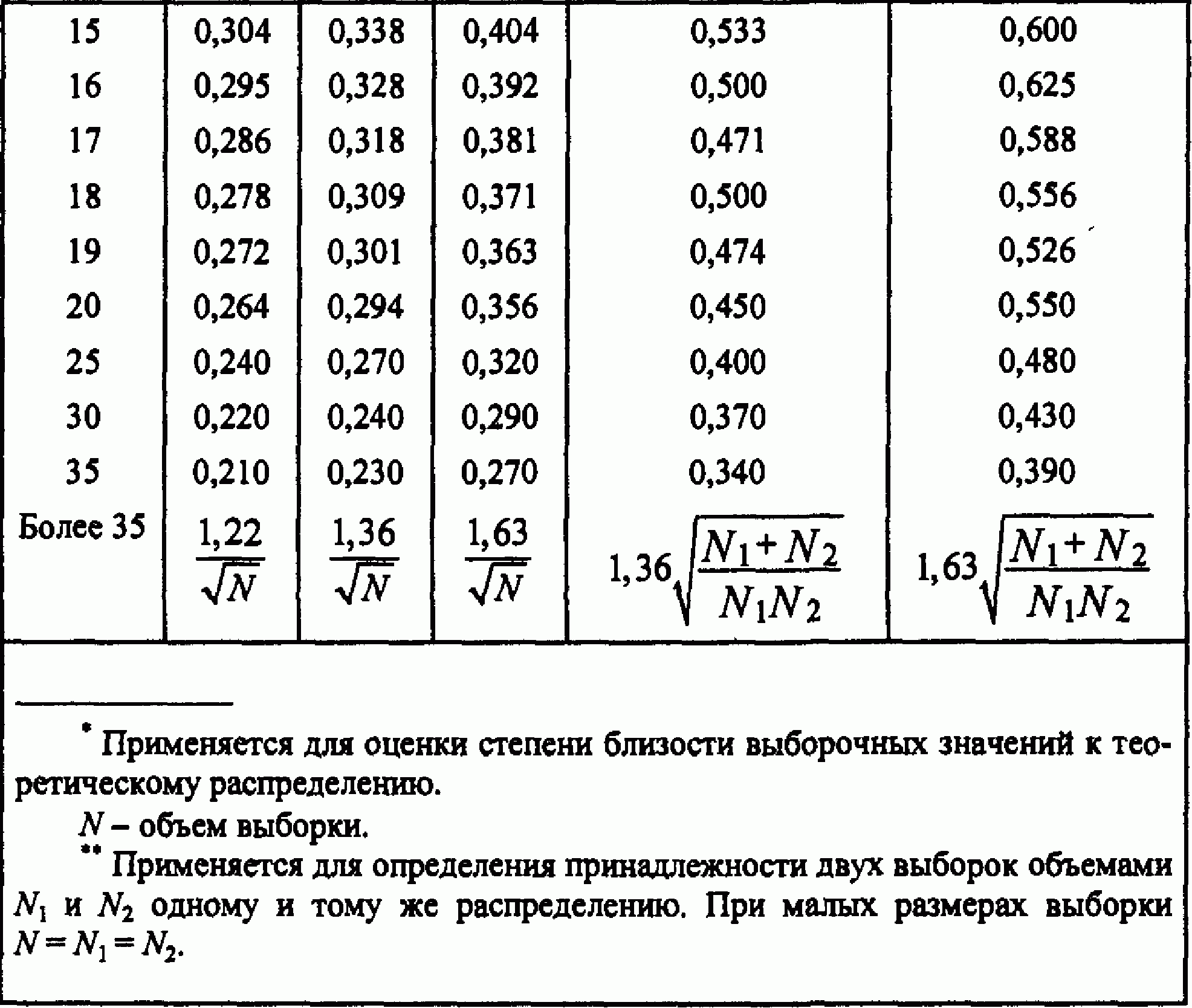
Алгоритм реализации критерия Колмогорова-Смирнова предполагает использование критического значения Dextr для проверки принятой гипотезы. Для этого используется приведенная ниже табл. 1.
Таблица 1
Решение
1. Критерий Хи-квадрат
1.1. Реализация в MathCad

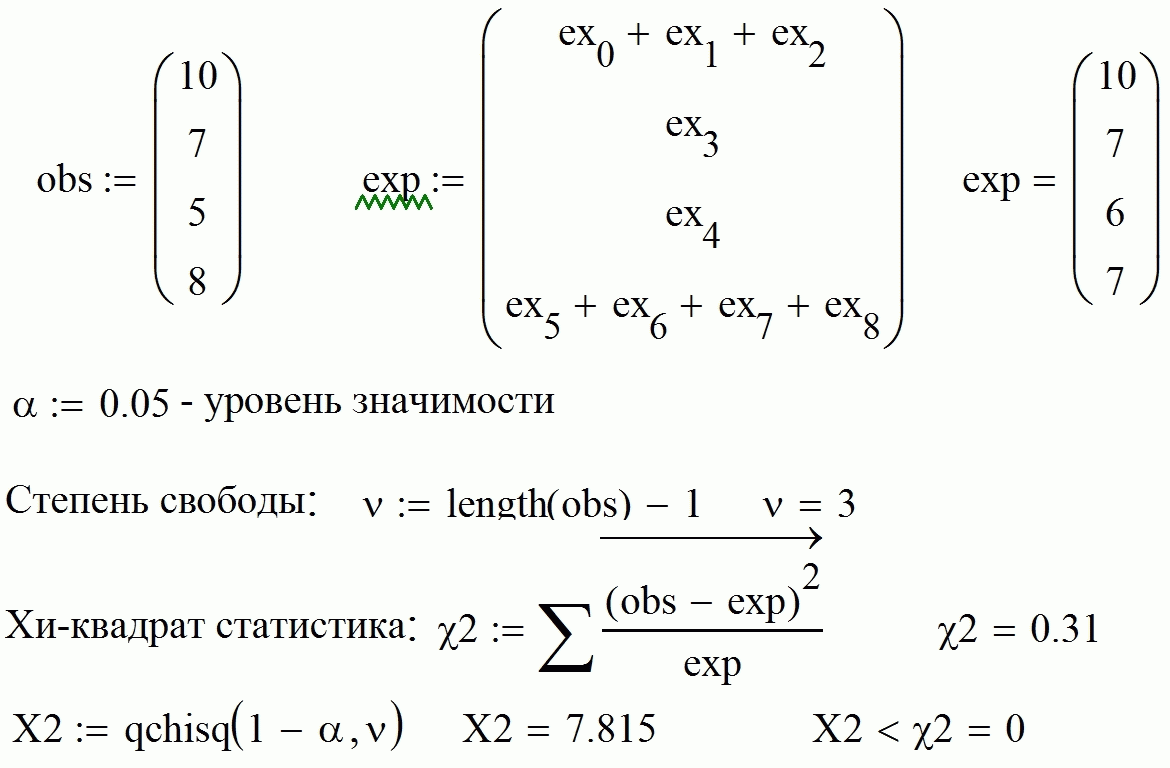
1.2. Реализация в Excel
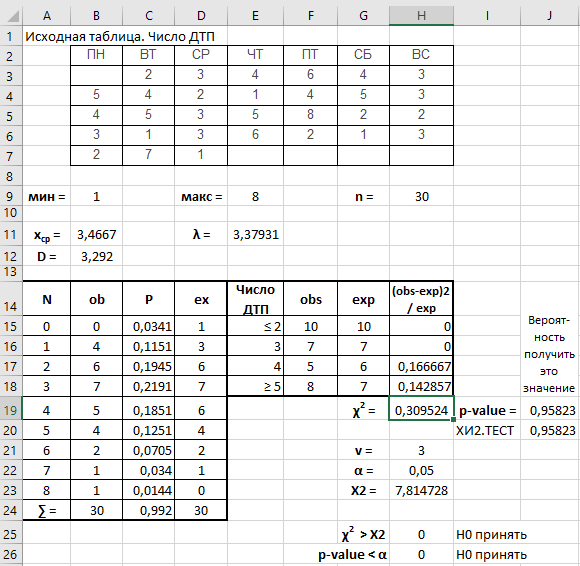
Формулы ячеек на листе Excel представлены в табл. 2.
Таблица 2
Формулы ячеек
| Ячейка | Характеристика | Формула |
| В15 | – число случаев исхода | =СЧЁТЕСЛИ($B$3:$H$7;A15) |
| С15 | – вероятность наступления | =ПУАССОН.РАСП(A15;$E$11;ЛОЖЬ) |
| D15 | – ожидаемое число случаев исхода | =ОКРУГЛ(C15*$H$9;0) |
| H19 | – статистика Хи-квадрат | =СУММ(H15:H18) |
| H23 | – критическое значение Хи-квадрата (максимальное значение для заданного уровня значимости) | =ХИ2.ОБР(1-H22;H21) |
| J19 | – p-value (вероятность получить расчетное значение Хи-квадрата) | =ХИ2.РАСП.ПХ(H19;H21) |
| J20 | – Хи-квадрат тест | =ХИ2.ТЕСТ(F15:F18;G15:G18) |
2. Критерий Колмогорова-Смирнова

Литература
- Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов: уч. пособ. - М.: Финансы и статистика, 2002. - 368с.
- Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с.
© В.Н. Кравченко
Последнее обновление: 2018.11.03
