| Главная » Статьи » Студентам » Мат. модели в трансф. экономике |
|
Классическим примером
динамической модели управления взаимодействием предприятий в цепи поставок
является теоретическая модель о пивоваренном заводе (The Beer Game simulation) и ее модификации [Agapova T., Fletcher E. Teaching Supply Chain Management through Simulation Modelling. –
Donetsk, Sunderland: REAP, TEMPUS/TACIS programme JEP number, 2002. – 9 p.; Sterman, J. Teaching takes off: Flight
simulators for management education: “The Beer Game" // http://web.mit.edu/jsterman/www/SDG/beergame.html.], которые иллюстрируют продвижение ТМЦ от производителя к дистрибьютору,
далее оптовому и розничному торговым предприятиям. Часть данных моделей
относится к классу непрерывных моделей, а
часть – к классу дискретных. В дискретных задачах ожидаемый
спрос в период времени t
описывается следующим разностным уравнением [Paul R.J., Hlupic V. and
Giaglis G., 1998.,
Simulation modeling of business processes. In: Avison D. and Edgar-Neville D.,
ed. Proceedings of the 3rd UK Academy of Information Systems Conference, June
1998. Lincoln: McGraw-Hill. – рр. 311-320.]:
где Характерной для данной модели и ее модификаций чертой
является использование каждым элементом цепи поставок параметра, регулирующего
интенсивность восполнения запасов на складе (
где
Таким образом, выполнение заказов на каждом
предприятии регулируется двумя параметрами: 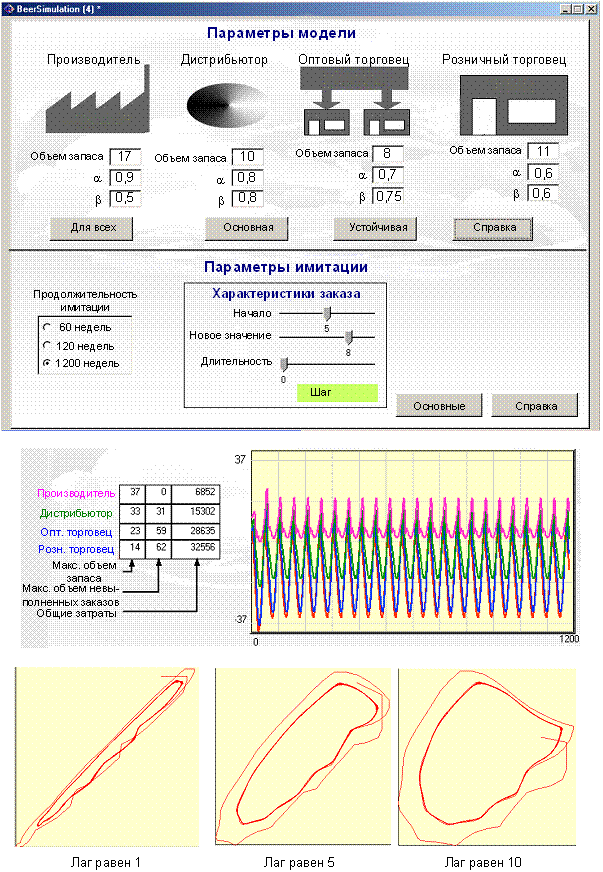 Рис. 1. Результаты реализации классической модели
"Beer Game" Анализ результатов моделирования позволяет сделать
вывод о том, что если во взаимодействии предприятий в цепи поставок ярко
выражен экономический сепаратизм, то они несут большие затраты вследствие
неурегулированного материального потока. Недостатком модели является то, что структура цепи
поставок является упрощенной – представлена в виде одного канала сбыта, не
учитывает производственные процессы поставщиков и процесс доставки сырья от них
предприятию-производителю (в данном случае на пивоваренный завод), а
следовательно, не учитывается снабженческая деятельность производителя. В анализе эффективности и процессе совершенствования
функционирования цепи поставок большое внимание уделяется временным
характеристикам, поскольку большие лаги в закупочной и сбытовой деятельности
приводят к повышению издержек (табл. 1) и способны дестабилизировать работу
системы [Törn A. Simulation nets, a simulation modeling and validation
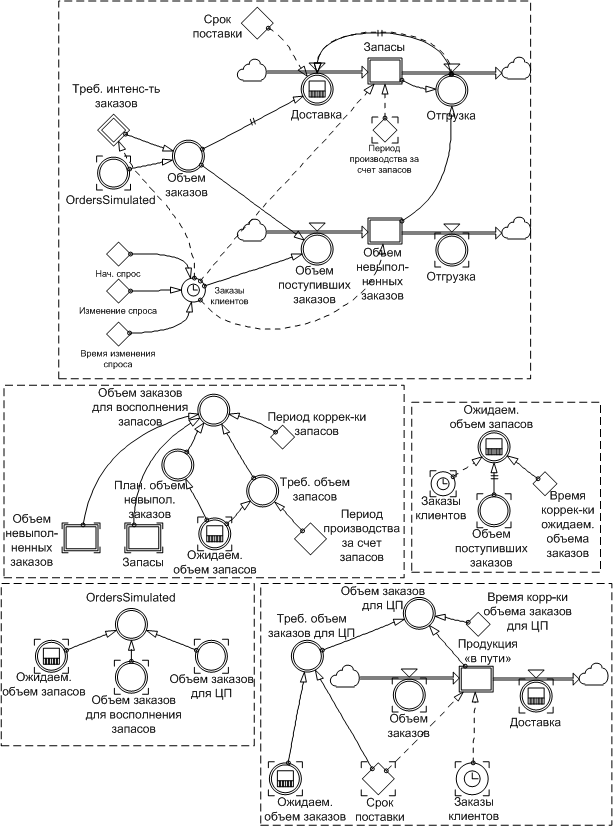
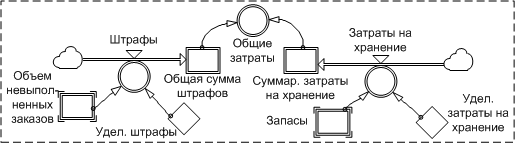
tool // Simulation. – 1985. – Vol. 45, No. 2. – pp.71-75.]. Таблица 1 Временные показатели в анализе цепей поставок  Для анализа влияния временных параметров работы цепи поставок и величин технологических запасов на предприятиях может быть использована модифицированная модель "Beer Game", которая охватывает распределительный канал из четырех элементов и реализована в терминах системной динамики (рис. 2) [Myrtveit M. Beer Distribution Game. – Massachusetts Institute of Technology, Powersim Corp, 1996.]. Модификация модели осуществлена посредством включения в модель параметров, отражающих временные периоды принятия решений и их реализации. Поиск оптимального варианта значений регулирующих параметров производится на основе стоимостной сравнительной оценки проведенных экспериментов. Итоговым показателем, который подлежит сравнению, являются общие издержки функционирования цепи поставок.
Рис.2. Модифицированная модель Beer Game в
терминах системной динамики [Myrtveit] Уравнения
диаграммы модели, построенной в ППП PowerSim: Объем невыполненных заказов: init Backlog = CustomerOrders flow Backlog = -dt*ShipmentsOut +dt*OrdersIn doc Backlog = невыполненные заказы (продукция не отгружена. Запасы: init Inventory =
InventoryCoverage*CustomerOrders flow Inventory =
-dt*ShipmentsOut+dt*ShipmentsIn doc Inventory = запас продукции. Продукция «в пути»: init OrdersInPipeline =
CustomerOrders*DeliveryDelay flow OrdersInPipeline =
-dt*ShipmentsIn +dt*OrdersOut doc OrdersInPipeline = количество заказанной, но не доставленной от
поставщиков продукции. Общая сумма штрафов: init SumCostBacklog = 0
{Currency} flow SumCostBacklog =
+dt*CostBacklog doc SumCostBacklog = общая сумма штрафов. Суммарные затраты на
хранение: init SumCostInventory = 0
{Currency} flow SumCostInventory =
+dt*CostInventory doc SumCostInventory = суммарные затраты на хранение. Штрафы: aux CostBacklog = Backlog *
UnitCostBacklog doc CostBacklog = сумма штрафов, начисляемая за задержку доставки
продукции на одну неделю. Затраты на хранение: aux CostInventory = Inventory *
UnitCostInventory doc CostInventory = затраты на хранение продукции в течение одной недели. Объем поступивших заказов: aux OrdersIn = CustomerOrders
WHEN p = FIRST(p) BUT OrdersOut(p-1) OTHERWISE doc OrdersIn = поступившие заказы. Первый участник цепи поставок
получает заказ непосредственно от покупателя, остальные – от предшествующих им участников цепи поставок. Объем акцептованных заказов: aux OrdersOut =
SELECTDECISION(INDEX(p), OrdersDecided, OrdersSimulated, OrdersSimulated,
OrdersSimulated) doc OrdersOut = объем акцептованных заказов. Доставка: aux ShipmentsIn =
DELAYPPL(ShipmentsOut(p+1), DeliveryDelay, ShipmentsOut(p+1)) WHEN p <
LAST(p) BUT DELAYPPL(OrdersOut(p), DeliveryDelay, ShipmentsOut(p)) OTHERWISE doc ShipmentsIn =объем
продукции, доставленной предприятию от его
поставщика. Отгрузка: aux ShipmentsOut =
MIN(Inventory, Backlog) doc ShipmentsOut = объем отгруженной продукции. Заказы клиентов: aux CustomerOrders =
CustomerOrdersInitial + STEP(CustomerOrdersStep,
CustomerOrdersStepTime)+STEP(CustomerOrdersStep, 100) doc CustomerOrders = объем продукции, заказанный конечными потребителями. Планируемый объем
невыполненных заказов, Требуемый объем запасов: aux DesiredBacklog =
ExpectedOrders aux DesiredInventory =
ExpectedOrders*InventoryCoverage doc DesiredInventory = требуемый объем запасов. Требуемый объем заказов для
цепи поставок: aux DesiredOrdersInPipeline =
ExpectedOrders*DeliveryDelay doc DesiredOrdersInPipeline = объем заказов, необходимый для выполнения заказов
участников цепи поставок в случае задержек поставок. Ожидаемый объем запасов: aux ExpectedOrders =
DELAYINF(OrdersIn(p), ExpectedOrdersAdjustmentTime, 1, CustomerOrders) doc ExpectedOrders = ожидаемое число заказов, рассчитанное путем
сглаживания темпа поступления заказов. Объем заказов для восполнения
запасов: aux OrdersForInventory =
(DesiredInventory - Inventory + Backlog - DesiredBacklog) /
InventoryAdjustmentTime doc OrdersForInventory = объем заказов для восполнения запасов. Объем заказов для цепи
поставок aux OrdersForPipeline =
(DesiredOrdersInPipeline - OrdersInPipeline) / OrdersForPipelineAdjustmentTime doc OrdersForPipeline = заказы для удовлетворения требований цепи поставок. Расчетный объем заказов: aux OrdersSimulated = MAX(0,
ROUND(OrdersForInventory + OrdersForPipeline + ExpectedOrders)) doc OrdersSimulated = расчетный объем заказов. Общие затраты: aux SumCost = SumCostBacklog +
SumCostInventory doc SumCost = сумма общих затрат предприятия. Начальный спрос: const CustomerOrdersInitial = 4
{Bottle/Week} doc CustomerOrdersInitial = начальный спрос. Уровень изменения спроса: const CustomerOrdersStep = 4
{Bottle/Week} doc CustomerOrdersStep = скачкообразное изменение спроса. Период изменения спроса: const CustomerOrdersStepTime = 2
{Week} doc CustomerOrdersStepTime = период, за который происходит скачкообразное изменение
спроса. Срок поставки: const DeliveryDelay = 6{Week} doc DeliveryDelay = период между отгрузкой и доставкой. Время корректировки
ожидаемого объема заказов: const ExpectedOrdersAdjustmentTime
= 4 {Week} doc ExpectedOrdersAdjustmentTime
= время, необходимое для корректировки
ожидаемого объема заказов. Период корректировки запасов: const InventoryAdjustmentTime = 5
{Week} doc InventoryAdjustmentTime = время, необходимое для корректировки запасов. Период производства за счет
запасов: const InventoryCoverage = 3 {Week} doc InventoryCoverage = время, в течение которого продолжение производства
возможно за счет имеющихся запасов при ожидаемом уровне заказов. Требуемая интенсивность
заказов: const OrdersDecided =
INIT(CustomerOrders) {Bottle/Week} doc OrdersDecided = установленная интенсивность заказов. Время корректировки объемов
заказов для цепи поставок: const OrdersForPipelineAdjustmentTime
= 10 {Week} doc OrdersForPipelineAdjustmentTime
= период времени корректировки объемов
заказов для цепи поставок. Удельные штрафы: const UnitCostBacklog = 10
{Currency/Bottle} doc UnitCostBacklog = удельные штрафы за невыполненные заказы. Удельные затраты на хранение: const UnitCostInventory = 5
{Currency/Bottle} | |
| Категория: Мат. модели в трансф. экономике | Добавил: kvn2us (21.03.2009) | | |
| Просмотров: 5275 |