| Главная » Статьи » Студентам » Логистика |
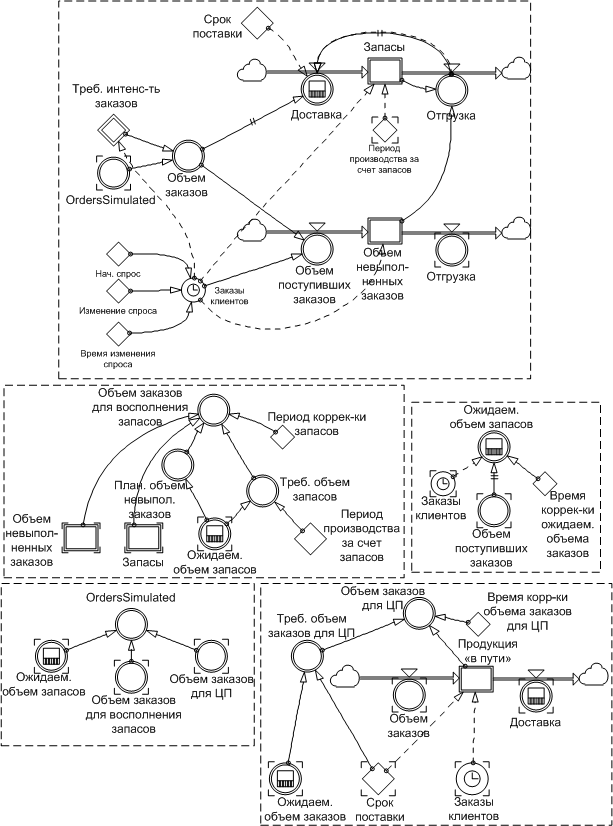
Системно-динамическая модель "Beer Game" Для анализа влияния временных параметров работы цепи поставок и величин технологических запасов на предприятиях может быть использована модифицированная модель "Beer Game", которая охватывает распределительный канал из четырех элементов и реализована в терминах системной динамики (рис. 1) [Myrtveit M. Beer Distribution Game. – Massachusetts Institute of Technology, Powersim Corp, 1996.]. Модификация модели осуществлена посредством включения в модель параметров, отражающих временные периоды принятия решений и их реализации. Поиск оптимального варианта значений регулирующих параметров производится на основе стоимостной сравнительной оценки проведенных экспериментов. Итоговым показателем, который подлежит сравнению, являются общие издержки функционирования цепи поставок.
Рис. 1. Модифицированная модель Beer Game в терминах системной динамики [Myrtveit] Объем поступивших заказов: aux OrdersIn = CustomerOrders WHEN p = FIRST(p) BUT OrdersOut(p-1) OTHERWISE Первый участник цепи поставок получает заказ непосредственно от покупателя, остальные – от предшествующих им участников цепи поставок. Объем акцептованных заказов: aux OrdersOut = SELECTDECISION(INDEX(p), OrdersDecided, OrdersSimulated, OrdersSimulated, OrdersSimulated) Доставка: aux ShipmentsIn = DELAYPPL(ShipmentsOut(p+1), DeliveryDelay, ShipmentsOut(p+1)) WHEN p < LAST(p) BUT DELAYPPL(OrdersOut(p), DeliveryDelay, ShipmentsOut(p)) OTHERWISE Это - объем продукции, доставленной предприятию от его поставщика. Объем заказов для восполнения запасов: aux OrdersForInventory = (DesiredInventory - Inventory + Backlog - DesiredBacklog) / InventoryAdjustmentTime | |
| Категория: Логистика | Добавил: kvn2us (21.03.2015) | | |
| Просмотров: 1279 | |