Регрессионный анализ

Часть 3. Множественная регрессия

Подготовка данных

Возьмем таблицу с именем “state.x77” и на ее основе определим новую таблицу states

> states<-data.frame(state.x77)

Подключим пакет “car”

> install.packages("car") # если пакет не установлен
> library(car)

Для того, чтобы понять структуру используемой таблицы данных выведем на экран ее шапку

> head(states)

           Population Income Illiteracy Life.Exp Murder HS.Grad Frost   Area
Alabama          3615   3624        2.1       69   15.1      41    20  50708
Alaska            365   6315        1.5       69   11.3      67   152 566432
Arizona          2212   4530        1.8       71    7.8      58    15 113417
Arkansas         2110   3378        1.9       71   10.1      40    65  51945
California      21198   5114        1.1       72   10.3      63    20 156361
Colorado         2541   4884        0.7       72    6.8      64   166 103766

Как видно, таблица отображает в разрезе каждого из 50 штатов США данные о:

• численности населения штата, по состоянию на 01.07.1975;
• доходах в 1974 г.;
• уровне грамотности, % от численности в 1970 г.;
• средней продолжительности жизни на основе данных 1969-71 гг.;
• уровне убийств (в расчете на 100 тыс. чел., 1976 г.);
• % людей, имеющих высшее образование в 1970 г.
• среднем количестве холодных дней (1931-1960);
• площади территории (кв. миль).

Сначала можно визуально представить, как соотносятся между собой переменные (рис. 3).

> scatterplotMatrix(states,spread = FALSE, lty.smooth = 2, main ='Соотношение всех переменных')

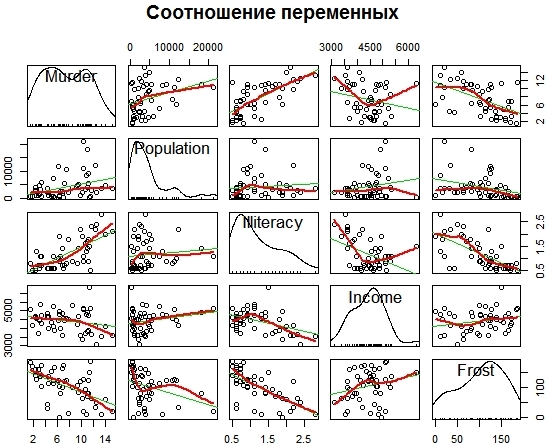
Рис. 3. Визуализация отношений между переменными

Чтобы увидеть зависимость уровня убийств по штатам (на примере США) от социально-экономических и прочих показателей, можно сократить количество графиков, учитывая только выборочные показатели – численность населения, грамотность, уровень доходов и количество холодных дней.

Для этого определим новую таблицу states1, а после построим графики зависимостей (рис. 4).

> states1 <- as.data.frame(state.x77[,c("Murder", "Population", "Illiteracy", "Income", "Frost")])

> scatterplotMatrix(states1, spread = FALSE, lty.smooth = 2, main ='Соотношение переменных')

Рис. 4. Соотношение между выбранными переменными

Анализ

Корреляция

К тому же полезной является корреляционная матрица

> cor(states)

           Population Income Illiteracy Life.Exp Murder HS.Grad  Frost   Area
Population      1.000   0.21      0.108   -0.068   0.34  -0.098 -0.332  0.023
Income          0.208   1.00     -0.437    0.340  -0.23   0.620  0.226  0.363
Illiteracy      0.108  -0.44      1.000   -0.588   0.70  -0.657 -0.672  0.077
Life.Exp       -0.068   0.34     -0.588    1.000  -0.78   0.582  0.262 -0.107
Murder          0.344  -0.23      0.703   -0.781   1.00  -0.488 -0.539  0.228
HS.Grad        -0.098   0.62     -0.657    0.582  -0.49   1.000  0.367  0.334
Frost          -0.332   0.23     -0.672    0.262  -0.54   0.367  1.000  0.059
Area            0.023   0.36      0.077   -0.107   0.23   0.334  0.059  1.000

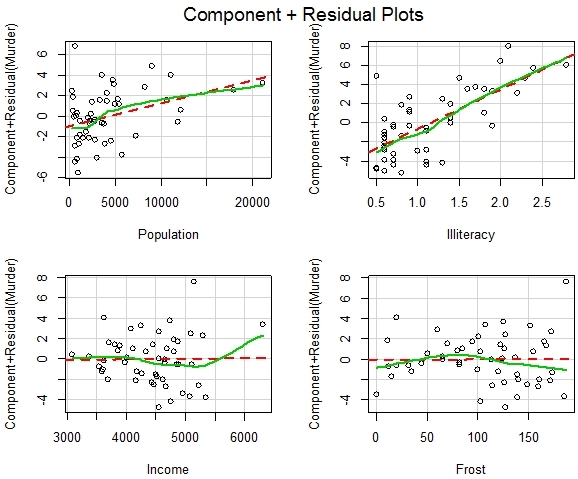
Модель множественной регрессии

Разработаем модель линейной множественной регрессии на основе переменных, выбранных в таблице states1

> fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states1)

> summary(fit)

Call:

lm(formula = Murder ~ Population + Illiteracy + Income + Frost, data = states1)

Residuals:
    Min      1Q  Median      3Q     Max
-4.7960 -1.6495 -0.0811  1.4815  7.6210 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.235e+00  3.866e+00   0.319   0.7510
Population  2.237e-04  9.052e-05   2.471   0.0173 *
Illiteracy  4.143e+00  8.744e-01   4.738 2.19e-05 ***
Income      6.442e-05  6.837e-04   0.094   0.9253
Frost       5.813e-04  1.005e-02   0.058   0.9541
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared:  0.567,   Adjusted R-squared:  0.5285 
F-statistic: 14.73 on 4 and 45 DF,  p-value: 9.133e-08

Доверительные интервалы

Найдем доверительные интервалы для параметров модели

> confint(fit)

                    2.5 %       97.5 %
(Intercept) -6.552191e+00 9.0213182149
Population   4.136397e-05 0.0004059867
Illiteracy   2.381799e+00 5.9038743192
Income      -1.312611e-03 0.0014414600
Frost       -1.966781e-02 0.0208304170

Значимы только Illiteracy (уровень грамотности) и Population (численность населения)

Тест Дарбина-Утсона

> durbinWatsonTest(fit)

 lag Autocorrelation D-W Statistic p-value
   1      -0.2006929      2.317691   0.268
 Alternative hypothesis: rho != 0

Тест показывает, что автокорреляция отсутствует.

Графики частичных остатков

Графики частичных остатков показывают связь между независимой переменной и зависимой (Murder) при условии, что остальные независимые переменные включены в модель (рис. 5). Для их построения воспользуемся записью

> crPlots(fit)

Рис. 5. Графики частичных остатков

© Источники:

1. rpubs.com
2. tutorialspoint.com
3. Доп. см.: coastal.edu