Регрессионный анализ

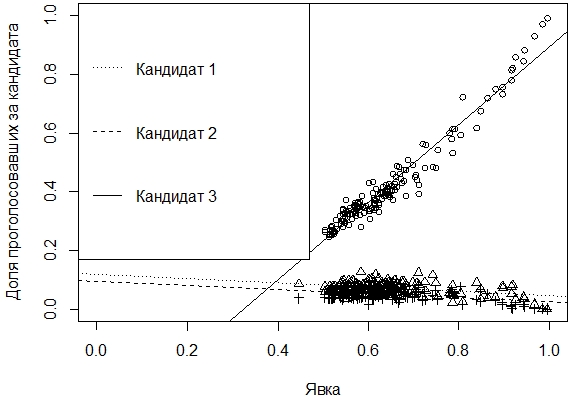
Часть 2. Сравнение регрессий

<<<Часть 1. Парная регрессия

Определение нескольких линейных моделей

Нередко требуется сравнить несколько регрессий на основе одних и тех же данных. Это подтверждается примером о результатах выборов, когда нужно проанализировать соответствие между процентом избирателей, проголосовавших за данного кандидата, и процентом явки на конкретном избирательном участке. Различие электоратов приводит к разным отношениям между указанными показателями. 

Возьмем данные из текстового файла, содержащего данные о результатах голосования за трех кандидатов по множеству участков.

> vybory <- read.table("vybory.txt", h=TRUE)
> str(vybory)

'data.frame':    153 obs. of  7 variables:
 $ UCHASTOK: int  1 2 3 4 5 6 7 8 9 10 ...
 $ IZBIR   : int  329786 144483 709903 696114 717095 787593 696087 691688 730050 164275 ...
 $ DEJSTV  : int  2623 859 5656 4392 3837 4715 10456 1819 2403 89 ...
 $ NEDEJSTV: int  198354 97863 664195 619629 653133 655486 397797 632045 667994 161470 ...
 $ KAND.1  : int  24565 7884 30491 54999 36880 72166 43559 53046 60355 234 ...
 $ KAND.2  : int  11786 6364 11152 11519 10002 25204 28189 5504 2680 451 ...
 $ KAND.3  : int  142627 68573 599105 525814 559653 485669 267776 563502 599798 159496 ...
 

Присоединим таблицу данных для того, чтобы с ее столбцами работать как с независимыми переменными:

> attach(vybory)

Вычислим доли проголосовавших за каждого кандидата и явку

> share<-cbind(KAND.1, KAND.2, KAND.3) / IZBIR
> att<-(DEJSTV+NEDEJSTV)/IZBIR

Рассчитаем корреляцию между явкой и долей

> cor(att, share)
         KAND.1   KAND.2    KAND.3
[1,] -0.3898262 -0.41416 0.9721124

Можно предположить небольшую корреляцию для первых 2 кандидатов и ее отличие от корреляции для 3-го кандидата.

Построим модели регрессии по всем кандидатам и выведем сведения о них

> lm.1 <- lm(share[,1] ~ att)
> lm.2 <- lm(share[,2] ~ att)
> lm.3 <- lm(share[,3] ~ att)
> lapply(list(lm.1, lm.2, lm.3), summary)

[[1]]

Call:
lm(formula = share[, 1] ~ att)

Residuals:
      Min         1Q        Median        3Q         Max 
-0.046133 -0.013211 -0.001493  0.012742  0.057943 

Coefficients:
             Estimate     Std. Error  t value   Pr(>|t|)    
(Intercept)  0.117115   0.008912  13.141    < 2e-16 ***
att            -0.070726   0.013597  -5.202   6.33e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.01929 on 151 degrees of freedom
Multiple R-squared:  0.152,    Adjusted R-squared:  0.1463 
F-statistic: 27.06 on 1 and 151 DF,  p-value: 6.331e-07

[[2]]

Call:
lm(formula = share[, 2] ~ att)

Residuals:
      Min        1Q        Median        3Q         Max 
-0.036542 -0.014191 -0.000162  0.011782  0.050139 

Coefficients:
             Estimate     Std. Error   t value   Pr(>|t|)    
(Intercept)  0.093487   0.007807  11.974   < 2e-16 ***
att            -0.066597   0.011911    -5.591 1.03e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0169 on 151 degrees of freedom
Multiple R-squared:  0.1715,    Adjusted R-squared:  0.166 
F-statistic: 31.26 on 1 and 151 DF,  p-value: 1.027e-07

[[3]]

Call:
lm(formula = share[, 3] ~ att)

Residuals:
      Min        1Q         Median        3Q        Max 
-0.116483 -0.023570  0.000518  0.025714  0.102810 

Coefficients:
            Estimate     Std. Error   t value     Pr(>|t|)    
(Intercept) -0.43006    0.01702  -25.27     <2e-16 ***
att             1.32261    0.02597   50.94     <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.03684 on 151 degrees of freedom
Multiple R-squared:  0.945,    Adjusted R-squared:  0.9446 
F-statistic:  2595 on 1 and 151 DF,  p-value: < 2.2e-16

Далее представим результаты регрессионного анализа графически

> plot(share[,3] ~ att, xlim=c(0,1), ylim=c(0,1), xlab="Явка", ylab="Доля проголосовавших за кандидата")
> points(share[,1] ~ att, pch=2)
> points(share[,2] ~ att, pch=3)
> abline(lm.3)
> abline(lm.2, lty=2)
> abline(lm.1, lty=3)
> legend("topleft", lty=c(3,2,1),legend=c("Кандидат 1","Кандидат 2","Кандидат 3"))

Графически предположение о различии модели регрессии по 3-му кандидату от моделей по первым двум подтверждается (рис. 1). 

Рис. 1. Линейные модели регрессии по каждому кандидату

В регрессионном анализе встречаются категориальные переменные (categorical variable), которые имеют значения «да» / «нет», «женский» / «мужской» и т.п. В примере о выборах данные можно представить таким образом, что категориальной переменной становится «кандидат». Для того, чтобы статистически сравнить регрессии с категориальными переменными (факторами, предикторами) применяется метод анализа ковариаций – ANCOVA.

Создание таблиц данных с категориальными переменными

Создадим новую таблицу данных, в которой 1 столбец – это явка, и назовем его «javka»; 2-й – доля («dolja»), а 3-й – фактор с именами кандидатов («kand»).

> vybory2 <- cbind(att, stack(data.frame(share)))
> names(vybory2) <- c("javka","dolja","kand")
> str(vybory2)

'data.frame':    459 obs. of  3 variables:
 $ javka: num  0.609 0.683 0.944 0.896 0.916 ...
 $ dolja: num  0.0745 0.0546 0.043 0.079 0.0514 ...
 $ kand : Factor w/ 3 levels "KAND.1","KAND.2",..: 1 1 1 1 1 1 1 1 1 1 ...

Рассмотрим алгоритм создания новой таблицы “vybory2”. Изначально имеем таблицу “share” – доли проголосовавших за каждого кандидата по всем избирательным участкам.

> head(share,3)

         KAND.1     KAND.2    KAND.3
[1,] 0.07448770 0.03573833 0.4324835
[2,] 0.05456697 0.04404670 0.4746095
[3,] 0.04295094 0.01570919 0.8439252

После выполнения stack() получаем таблицу, в которой один столбец – значения доли, а второй – имя кандидата. Сначала выводятся данные по 1-му кандидату, потом – по 2-му и, наконец, все значения по 3-му.

>head(stack(data.frame(share)),3)

      values    ind
1 0.07448770 KAND.1
2 0.05456697 KAND.1
3 0.04295094 KAND.1

Далее в полученную таблицу добавили столбец ”att” – явка, в котором значения расположены таким же образом – сначала по 1-му кандидату, потом по 2-му, и, наконец, по 3-му. Поэтому строк (наблюдений) в новой таблице насчитывается 459 шт.

> head(vybory2, 3)

       javka        dolja          kand
1 0.6094164 0.07448770 KAND.1
2 0.6832776 0.05456697 KAND.1
3 0.9435810 0.04295094 KAND.1

После создания новой таблицы переходим к анализу. При этом будем использовать две функции lm() и aov().

1. lm() 

> ancova.v <- lm(dolja ~ javka * kand, data=vybory2)
> summary(ancova.v)

Call:
lm(formula = dolja ~ javka * kand, data = vybory2)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.116483 -0.015470 -0.000699  0.014825  0.102810 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       0.117115   0.011973   9.781  < 2e-16 ***
javka            -0.070726   0.018266  -3.872 0.000124 ***
kandKAND.2       -0.023627   0.016933  -1.395 0.163591    
kandKAND.3       -0.547179   0.016933 -32.315  < 2e-16 ***
javka:kandKAND.2  0.004129   0.025832   0.160 0.873074    
javka:kandKAND.3  1.393336   0.025832  53.938  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02591 on 453 degrees of freedom
Multiple R-squared:  0.9824,    Adjusted R-squared:  0.9822 
F-statistic:  5057 on 5 and 453 DF,  p-value: < 2.2e-16

Анализ ковариаций использует формулу модели 

отклик ~ воздействие * фактор,

где звездочка «*» обозначает, что надо проверить одновременно отклик на воздействие, отклик на фактор и взаимодействие между воздействием и фактором. Следует отметить, что линейная регрессия использует более простую формулу

«отклик ~ воздействие».

В нашем случае откликом была доля проголосовавших, воздействием – явка, а фактором – имя кандидата. Больше всего нас интересовало, правда ли, что имеется сильное взаимодействие между явкой и третьим кандидатом. Полученные результаты (см. строку javka:kandKAND.3) доказывают значимость этого взаимодействия.

2. aov() 

С взаимодействием фактора и предиктора

> ancova.v2 <- aov(dolja ~ javka * kand, data=vybory2)
> summary(ancova.v2)

             Df Sum Sq Mean Sq F value Pr(>F)    
javka         1  0.943   0.943    1404 <2e-16 ***
kand          2 13.440   6.720   10006 <2e-16 ***
javka:kand    2  2.597   1.299    1934 <2e-16 ***
Residuals   453  0.304   0.001                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Из представленных результатов видно, что значимыми являются и воздействие javka, и фактор kand, и их взаимодействие, поскольку P-значение меньше 0,05.

Без взаимодействия фактора (категориальной переменной) и предиктора

> ancova.v3 <- aov(dolja ~ javka + kand, data=vybory2)
> summary(ancova.v3)

              Df Sum Sq Mean Sq F value Pr(>F)    
javka         1  0.943   0.943   147.8 <2e-16 ***
kand          2 13.440   6.720  1053.8 <2e-16 ***
Residuals   455  2.902   0.006                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Сравнение

Сравним две модели (с и без взаимодействия фактора и предиктора), чтобы окончательно убедиться, является ли взаимодействие на самом деле статистически значимым. Для этого воспользуемся anova()

> anova(ancova.v2,ancova.v3)

Analysis of Variance Table

Model 1: dolja ~ javka * kand
Model 2: dolja ~ javka + kand
  Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
1    453 0.30422                                  
2    455 2.90163 -2   -2.5974 1933.8 < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Поскольку F-значение намного больше 1, а Р-значение меньше 0,05, то приходим к выводу, что взаимодействие является значимым. К тому же, сумма квадратов остатков (RSS) для модели с взаимодействием меньше, чем для модели без него.

В дополнение можно посмотреть на результаты anova() для ancova.v2 ancova.v3 по-отдельности.
 

© Источники:

1. Шипунов А. Б., Балдин E. М., Волкова П. А., Коробейников А. И., Назарова С. А., Петров С. В., Суфиянов В. Г. (2014) Наглядная статистика. Используем R! – 296 с. URL: ashipunov.info

2. tutorialspoint.com

3. Доп. см.: coastal.edu

<<< Часть 1. Парная регрессия