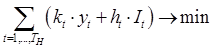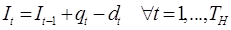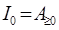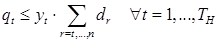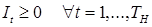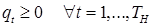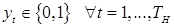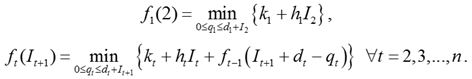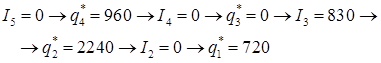| Главная » Статьи » Студентам » Логистика |
Однопродуктова динамічна модель управління запасами з детермінованим попитом
Постановка динамічної задачіЗагальні відомості Формула Вільсона (R.H. Wilson) дозволяє визначити економічний розмір замовлення в тих випадках, коли витрати на здійснення замовлення або налагоджувальні роботи та зберігання запасів можна порівняти з витратами по збуту продукції, попит на яку є постійним протягом всього періоду планування (дуже слабкі коливання можна відкинути). Але вона не дозволяє враховувати взаємозв'язки між окремими плановими випусками продукції та дефіцит виробничих потужностей. Тому, коли відомо, що попит суттєво змінюється протягом різних інтервалів горизонту планування, то за цією формулою можна отримати наближені або й зовсім неадекватні ситуації значення розмірів замовлення, що призводить до більших витрат. Коли замовлення формуються на майбутнє, та можна припустити детермінований нерівномірний характер динаміки попиту, тоді доцільним є побудова і вирішення динамічних оптимізаційних задач, спрямованих на мінімізацію логістичних витрат. Для визначення економічного розміру замовлення на закупівлю або виготовлення одного виду товару можна використовувати методи динамічного програмування. У 1958 р. Вагнером і Уайтіном (H.M. Wagner & T.M. Whitin) було здійснено загальну постановку динамічної моделі управління запасами одного виду продукції. Суть задачі полягає у визначенні розміру замовлення в кожному періоді часу таким чином, щоб забезпечити мінімальні сукупні логістичні витрати. Ця модель не припускає утворення заборгованостей перед споживачами потрібної продукції, а також обмеження на розмір замовлення (партії виробництва). Математичний записНехай 1, ..., TH – кінцевий дискретний горизонт планування; dt – величина попиту в період часу t; k – фіксовані витрати на здійснення замовлення; h – витрати на зберігання; It – обсяг запасу в період часу t; qt – розмір замовлення на поповнення запасу продукції в період t; yt – змінна, яка відповідає за рішення щодо відправки замовлення на поповнення запасу в період часу t. Цільова функція згаданої динамічної моделі має вигляд:
При цьому враховуються наступні обмеження: 1) динаміка обсягу запасу задана рівнянням:
2) для вирішення задачі треба вказати початкове значення обсягу запасу:
3) обсяг замовлення і, відповідно, поставки не можуть бути більшими, ніж обсяг попиту протягом проміжку часу t, що залишився згідно з горизонтом планування. Так, в 1-му періоді часу припустимо придбати продукцію в обсязі, що не перевищує розмір потреби на весь горизонт планування. В 2-му періоді часу (t=2) замовлення може або не робитись, тобто q2=0, або дорівнювати будь-якому значення, але не більшому ніж потреба на весь проміжок часу, що залишився, за винятком потреби в 1-му періоді (t=1). Отже:
4) такі величини, як обсяг запасу і розмір замовлення не можуть бути меншими нуля:
5) змінна yt приймає значення – 0 або 1:
ПрикладЗадачаКомпанія «Новопак» є виробником поліетиленової плівки. Відділ маркетингу та збуту підготував план продажів на наступний рік (табл. 1).
Таблиця 1
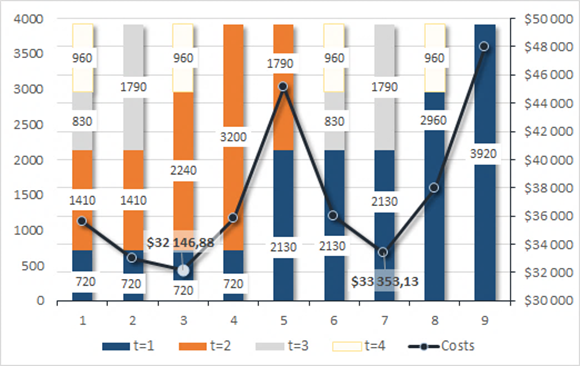
Витрати на налагодження виробництва (k) є постійними для всіх періодів часу та дорівнюють $8 900: kt = k = $8900. Безумовно, це є спрощенням задачі, як і те, що питомі витрати на зберігання продукції протягом горизонту планування теж є постійними. Для їх розрахунку враховуються ціна однієї паллети (с) та відсоткова ставка (p): с = $350 і p = 7,5%. Спираючись на цю інформацію потрібно визначити оптимальну політику виробництва, а саме: вказати, коли та скільки (у паллетах) потрібно виготовити продукції, щоб мати найменші сукупні витрати, що складаються з витрат на налагодження технологічної лінії та витрат на зберігання виготовленої продукції. На початок 1-го кварталу залишків продукції немає, тобто I0 = 0. РішенняЦя задача може вирішуватись завдяки постановці однопродуктової динамічної моделі управління запасами з детермінованим попитом і її реалізації за допомогою методу динамічного програмування, а в певних випадках – з використанням «Пошук рішень» в ППП «Excel». Сценарії розміщення замовлень Низка можливих сценаріїв замовлень, які відрізняються за періодами і кількостями товару, що надходить до складу, характеризується різними сукупними витратами, що складаються з витрат на наладку виробництва та витрат на зберігання товару на складі (рис. 1). Так, за 3-м сценарієм календарного графіку виробництва компанія понесе ці витрати в сумі $32 147, а за 7-м сценарієм – $33 353. Календарний графік у 3-му сценарії має наступний вигляд: у 1-му кварталі (t1) виготовляється 720 паллет; у 2-му – 2240; 3-му – 0; і, нарешті, у 4-му кварталі (t4) виготовляється 960 паллет.
Рис. 1. Витрати на наладку виробництва та зберігання товару за можливими сценаріями замовлень
Динамічне програмуванняЗастосуємо метод динамічного програмування, щоб перевірити, чи дійсно компанія несе мінімальні сукупні витрати саме за 3-м сценарієм. Оскільки дефіцит продукції не припустимий, задача зводиться до обчислення значень qt, які мінімізують сумарні витрати, пов’язані з розміщенням замовлень, закупівлею та зберіганням продукції протягом n етапів. Витрати на зберігання на t-му етапі для простоти вважаються пропорційними величині: It+1 = It + qt – dt. Ця величина являє собою обсяг запасу, що переходить із етапу t до етапу t+1. Введемо ft(It+1) – функцію мінімальних загальних витрат на етапах 1, 2, …, t на підставі величини запасу It на кінець етапу t. Тоді рекурентне рівняння алгоритму прямої прогонки буде записано наступним чином:
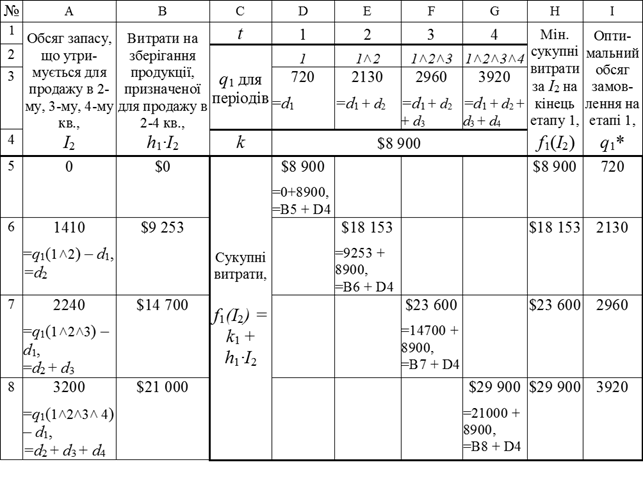
Поетапна реалізація вирішення поставленої задачі методом динамічного програмування наведено в табл. 2-5. Слід зазначити, що на будь-якому етапі t оптимальний обсяг замовлення qt* повинен дорівнювати нулю або попиту одного або більше наступних етапів. При позитивному початковому рівні запасу (I0 > 0) цей обсяг може бути списаним з попиту наступних етапів, доки він не вичерпається. Таблиця 2 Етап 1: d1 = 720, 0 ≤ I2 ≤ 3200, 720 ≤ q1 ≤ 3920 Таблиця 3 Етап 2: d2 = 1410, 0 ≤ I3 ≤ 1790, 0 ≤ q2 ≤ 3200 Таблиця 4 Етап 3: d3 = 830, 0 ≤ I4 ≤ 960, 0 ≤ q3 ≤ 1790 Таблиця 5 Етап 4: d4 = 830, 0 ≤ I5 ≤ 0, 0 ≤ q4 ≤ 960
Оптимальний календарний графік виробництва продукції визначається, як:
Отже, 3-й сценарій є оптимальним:
Загальні витрати за цим сценарієм складають $32 147.
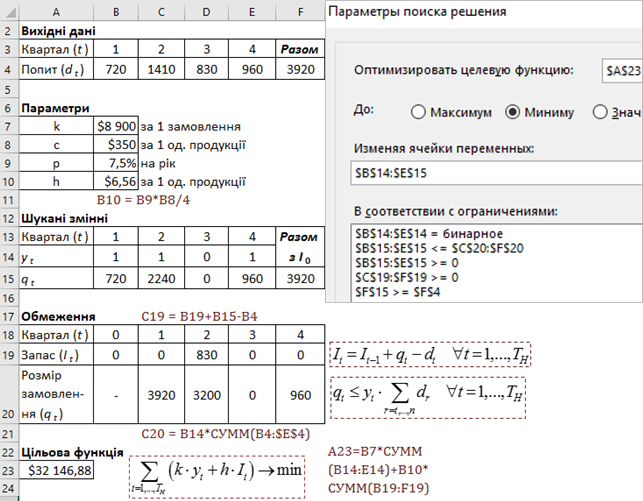
Пошук рішення в MS Excel 2016Далі застосуємо «Пошук рішення» для визначення оптимального графіка постачань. Рис. 2 ілюструє постановку та вирішення викладеної вище моделі на листі табличного редактору «Excel». На ньому виділені:
Рис. 2. Вирішення динамічної задачі управління запасами
Отримане оптимальне рішення співпадає з календарним графіком за 3-м сценарієм. Шукані змінні вказують на те, що продукція виготовляється в 1, 2 і 4-му кварталах в обсягах 720, 2240 і 960 паллет, відповідно. Цільова функція свідчить, що в такому випадку компанія понесе $32 147 загальних витрат.
| |||||||||||||
| Категория: Логистика | Добавил: kvn2us (03.07.2016) | | |||||||||||||
| Просмотров: 3496 | | |||||||||||||