| Главная » Статьи » Студентам » Основы научных исследований |
Метод регресійного аналізу в MS Excel
Задача регресійного аналізуВикористовуючи дані завдання (рис. 1), проведемо регресійний аналіз за допомогою вбудованого в MS Excel модуля "Регресія".
 Рис. 1. Вихідна інформація
Звіт регресійного аналізу в MS Excel
Загальний вигляд звітуНа рис. 2 наведено звіт регресійного аналізу в MS Excel з зазначенням зв’язків між характеристиками.
Рис. 2. Звіт регресійного аналізу в MS Excel Дисперсійний аналіз у звітіdf – діапазон В12:В14 на листі звіту, зображеного на рис. 2 – кількість ступенів свободи пов’язано з кількістю одиниць сукупності n і з кількістю констант (k+1), що визначається за нею. Чарунка С12 (рис. 2) містить пояснену суму квадратів (SS), зумовлену регресією:
Введемо
що є відхиленням істинного значення поясненої змінної від модельного значення для i-го спостереження. Тоді чарунка С13 містить залишкову суму квадратів, що пояснює відхилення від регресії:
Таким чином, метод найменших квадратів полягає у виборі такого набору коефіцієнтів серед усіх можливих, що забезпечує мінімальне значення SSoст.
Якщо всі коефіцієнти моделі, окрім константи
тобто ця константа дорівнює середньому значенню поясненої змінної. У такому випадку сукупна сума квадратів – чарунка С14 – дорівнює: 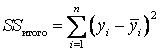 або
Вибіркове значення F, що має розподіл Фішера, у чарунці Е12, застосовується для оцінки надійності моделі в цілому, значущості коефіцієнта детермінації F і значущість F (F12) дозволяють перевірити значущість рівняння регресії, тобто встановити відповідність результатів регресійної моделі емпіричним даним і достатність незалежних змінних, внесених до неї, для опису залежної змінної. За емпіричним значенням статистики F перевіряється гіпотеза рівності нулю всіх коефіцієнтів моделі одночасно. Значущість F (F12) – це теоретична імовірність того, що при виконанні цієї гіпотези F-статистика більше емпіричного значення F. Потрібно, щоб Значущість F < 0.05. Рівняння регресії значимо на рівні де
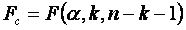 . .
Регресійна статистикаМножинний R (B4) – це коефіцієнт кореляції Пірсона. Застосовується при оцінці точності регресійної моделі. Його значення має перевищувати 0.7: R > 0,7. Коефіцієнт детермінації R2 > 0,5. Нормований (скоригований чи адаптований) коефіцієнт детермінації в чарунці В6 визначається наступним чином: 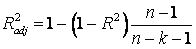 На відміну від Стандартна помилка (B7 і F37), позначимо SE, використовується для оцінки точності моделі шляхом розрахунку дроби, яка не повинна перевищувати 0,3 (30%): SE / (ymax – ymin) < 0,3,
Параметри рергесійного рівнянняВ чарунках D18:D19 надана t-статистика або, іншими словами, коефіцієнти Стьюдента. В оцінці надійності моделі для кожної з незалежних змінних (xi) значення коефіцієнтів Стюдента мають бути більше 2: ts > 2. P-значення (F18:F19) – імовірність, що дозволяє визначити значущість коефіцієнтів регресії Якщо P-значення більше або дорівнює Отже, для оцінки надійності моделі, необхідно, щоб для незалежних змінних (xi) виконувалась умова: p < 0,05. Нижні95%, Верхні95% (G17:H19) – довірчий інтервал для параметру
В оцінці надійності беруть до уваги, що довірчий інтервал не повинен містити 0.
Ці три показника є взамопов’язаними. Їх інтерпретація є однаковою: незалежні змінні (xi) мають значущій вплив на залежну змінну (y).
Оцінка адекватності моделі здійснюється за коефіцієнтом автокореляції (r). При цьому важливо, щоб він прагнув до нуля, а його критичне значення дорівнює 0,3:
r → 0, r < 0,3.
Коефіцієнт автокореляції r розраховується як коефіцієнт кореляції для двох наборів даних їх одного стовпчика. Дивлячись на рис. 2, визначаємо перший набір, як значення з 1 по 9 (передостанній), а другий набір – значення з 2 по 10 (останній).
| |
| Категория: Основы научных исследований | Добавил: kvn2us0758 (29.08.2009) | | |
| Просмотров: 17777 | |


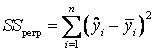
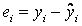 ,
, .
.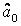
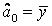 ,
,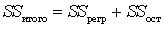 .
. .
.