| Главная » Статьи » Студентам » Имитационное моделирование |
ЗАДАНИЕ Группы заявок на расходование товара со
склада поступают через одинаково распределенные целочисленные случайные
промежутки времени t. Размер заявки - целочисленная случайная
величина Р. Если уровень запаса на складе ниже некоторой величины h, то
производится заказ величиной H, выполняющийся
с случайным запаздыванием Θ. Система с
ожиданием. Допускается частичное удовлетворение заявок. Построить
вероятностно-автоматную модель (ВАМ) для определения среднего количества товара
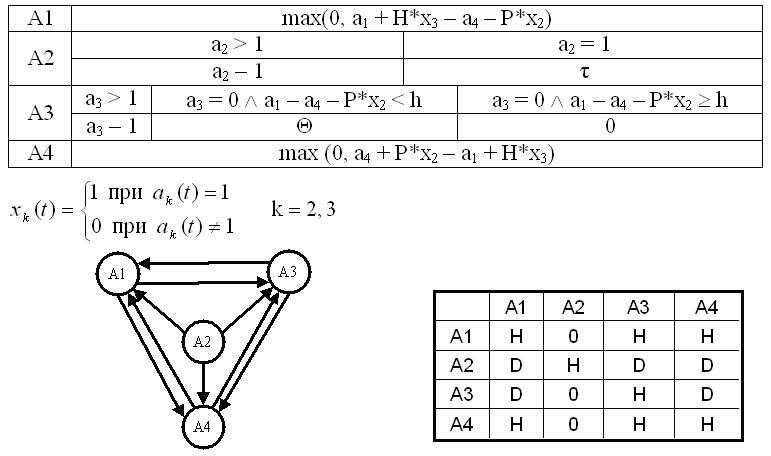
на складе. Построить граф межавтоматных связей,
матрицу алфавитов и матрицу структуры. Задать вектор начальных состояний. Осуществить расчет по модели при
различных значениях переменных.
Исследовать чувствительность модели. РЕШЕНИЕ
Введем обозначения: a1(t) – уровень запаса на складе в
момент времени t; a2(t) – промежуток времени,
оставшийся в момент t до поступления очередной заявки; a3(t) – промежуток времени,
оставшийся в момент t до очередного пополнения запаса, если к моменту t был
осуществлен заказ; a4(t) – наличие неудовлетворенного спроса в момент времени t. Определим событийные автоматы:
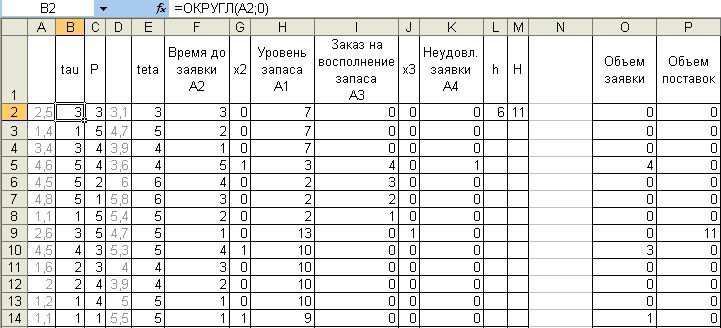
Реализуем имитацию модели в ППП "Excel"
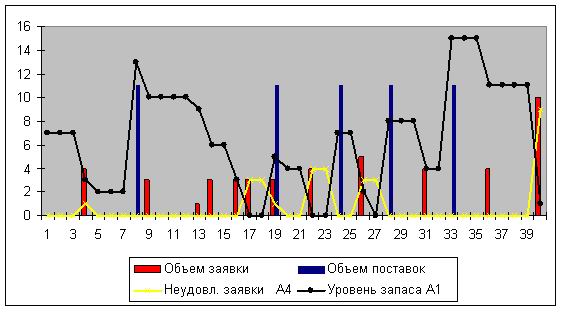
Формулы в ячейках: F2 = B2; F2 = ЕСЛИ(F2>1;F2-1;B3); G2 = 0; G3 = ЕСЛИ(F2=1;1;0); H2 = 7; H3 = (МАКС(0;H2+$M$2*J3-K2-C3*G3)); I2 = 0; I3 = ЕСЛИ(I2>1;I2-1;ЕСЛИ(И(I2=0;H3-K3-C3*G3<$L$2);E3;0)); J2 = 0; J3 = ЕСЛИ(I2=1;1;0); K2 = 0; K3 = МАКС(0;K2+C3*G3-H3+M2*J3); 02 = C2*G2; P2 = $M$2*J2. Графики изменения величин модели
| |
| Категория: Имитационное моделирование | Добавил: kvn2us (02.07.2009) | | |
| Просмотров: 3418 | |