| Главная » Статьи » Студентам » Бизнес-аналитика |
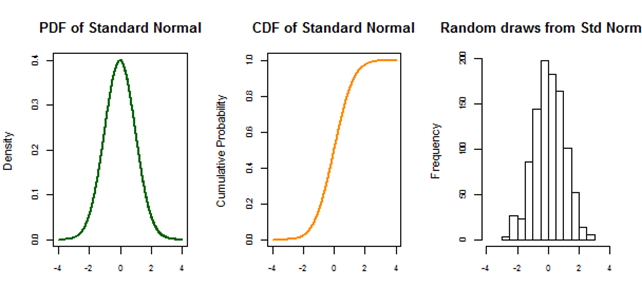
Случайная величина. Графики и T-testГрафики плотности вероятностей и интегральной функции распределения случайной величиныПостроим графики функций плотности и нормального распределения случайной величины. Всякий раз, когда вы используете функции вероятности, вы, как правило, должны помнить о необходимости установки начала (seed). Это означает блокировку в последовательности «случайных» (псевдослучайных) чисел, которые дает R, чтобы позже вы смогли воспроизвести свою работу. > set.seed(3000) Создадим набор последовательных значений чисел от -4 до 4 с шагом 0.01 > xseq<-seq(-4,4,.01) Величине densities назначаем функцию плотности вероятностей dnorm() – Probability Density Function, PDF – с параметрами mean = 0 и sd = 1 > densities<-dnorm(xseq, 0,1) Аналогично, величине cumulative присваиваем (кумулятивную) интегральную функцию распределения вероятностей pnorm() > cumulative<-pnorm(xseq, 0, 1) С помощью функции rnorm() сгенерируем 1 тыс. случайных величин в соответствии со стандартным нормальным законом распределения > randomdeviates<-rnorm(1000,0,1) Параметры par() создают область построения графиков в виде 1 строки и 3 столбцов (mfrow) и перемещают три графика ближе друг к другу (mar). > par(mfrow=c(1,3), mar=c(3,4,4,2)) Переходим к построению графиков функций плотности вероятностей и функции распределения вероятностей > plot(xseq, densities, col="darkgreen",xlab="", ylab="Density", type="l",lwd=2, cex=2, main="PDF of Standard Normal", cex.axis=.8) > plot(xseq, cumulative, col="darkorange", xlab="", ylab="Cumulative Probability",type="l",lwd=2, С помощью функции hist() построит гистограмму случайной величины с именем randomdeviates > hist(randomdeviates, main="Random draws from Std Normal", cex.axis=.8, xlim=c(-4,4)) После выполнения кода получим следующий графический результат (рис. 1)
Рис. 1. Графики плотности и интегрального распределения вероятностей; гистограмма случайной величины © Источник: r-bloggers.com
t-testРассмотрим t-критерий Стьюдента, который реализуется в R посредством t.test(). Знак «?» перед функцией (командой) вызывает справку о ней > ?t.test Имеются исходные данные о весе и росте 6 человек > weight<-c(60,72,57,90,95,72) На их основе рассчитаем индекс массы тела – вес человека, деленный на квадрат его роста > bmi<-weight/height^2 Предположим, что средний индекс массы тела равен 22,5. Тогда t.test(bmi,mu=22.5) One Sample t-test data: bmi
© Источник: Peter Dalgaard (2008). ‘Introductory Statistics with R’. Second Edition, Springer Science e+Business Media, LLC. 363 p. | |
| Категория: Бизнес-аналитика | Добавил: kvn2us (27.03.2017) | | |
| Просмотров: 1317 | |