| Главная » Статьи » Студентам » Имитационное моделирование |
|
Значительную часть теории очередей составляют методы определения характеристик СМО, находящихся под воздействием простейших потоков случайных событий. Поток однородных событий называется простейшим, если он обладает следующими тремя свойствами. Стационарность. Для любого положительного t (t>0) всегда существует такое k>=0,
что вероятность появления k
событий за период времени (a,
a+t), обозначим ее через pk(t), является одной и той же для
всех a>=0. Для потоков, в которых за
конечный промежуток времени с вероятностью 1 происходит конечное число событий,
всегда выполняется равенство Отсутствие последействия. Оно выражает собой отсутствие взаимной зависимости появления событий в потоке в непересекающихся между собой промежутках времени. В данном случае условная вероятность появления k событий (в зависимости от возможных вариантов чередования до начального момента времени a) за промежуток времени (a, a+t) равняется безусловной вероятности pk(t). Таким образом, появление в потоке очередного события не зависит от чередования предшествующих моменту a событий и как давно произошло последнее из них. Ординарность. Это означает, что вероятность появления в
стационарном потоке за промежуток времени В итоге получаем следующее окончательное определение простейшего потока. Определение 15. Простейшим потоком однородных событий называем всякий стационарный ординарный поток без последействия. Одной из характеристик потока случайных событий является его интенсивность – среднее число событий, происходящих в единицу времени. СМО обладают тем или иным свойством, но не всегда ограничиваются указанным выше набором. Впрочем, могут и не содержать в себе ни одного из приведенных свойств. Например, вполне вероятно, что интенсивность потока покупателей в магазин, торгующий исключительно зимней обувью или одеждой, зависит от времени года. Такой поток уже не является стационарным. На этом же примере можно показать, что свойство ординарности нарушается в том случае, когда происходит одновременное поступление нескольких заказов на приобретение товара от разных покупателей. Замечание 4. При поступлении заявок группами, их объем может быть как постоянным, так и случайным. В случае неординарного потока заявок в виде партий с постоянным размером рекомендуется переходить к ординарному потоку групповых заявок. Основная задача теории простейшего потока состоит в определении закона распределения числа событий за период времени t, рассматриваемый в качестве случайной величины. Это соответствует задачи отыскания функции pk(t). Однако сначала определим ее с фиксированным t. Возьмем интервал (0,1) и разобьем его произвольно на n равных частей. Длина каждой i-й части равна 1 / n. Так как поток обладает свойством отсутствия последействия, а, следовательно, события и их вероятности являются несовместными, то вероятность того, что за весь период t не поступит ни один клиент, определяется как Предположим откуда выразим вероятность того, что за промежуток времени дины 1 / n не поступит ни один клиент: Если период времени, равный k / n, где k – целое положительное число ( Пусть и из предположения, что p0(t) является невозрастающей функцией, поскольку, чем больше промежуток времени, тем меньше вероятность отсутствия клиентов, имеем В соответствии с (6) Так как
Рис. 5.8. Следовательно, для любого
стационарного потока без последействия функцию p0(t) можно
выразить через | |
| Категория: Имитационное моделирование | Добавил: kvn2us (10.02.2009) | | |
| Просмотров: 8322 |

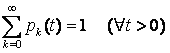 .
Таким образом, сущность данного свойства заключается в постоянстве
вероятностного режима во времени, или другими словами, вероятностные
характеристики потока не зависят от времени.
.
Таким образом, сущность данного свойства заключается в постоянстве
вероятностного режима во времени, или другими словами, вероятностные
характеристики потока не зависят от времени.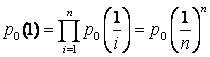 .
.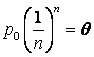 ,
,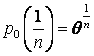 .
.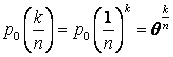 .
.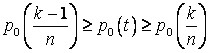 .
.