| Главная » Статьи » Студентам » Имитационное моделирование |
5.3 Характеристики простейшего потока событий (окончание)
начало Перейдем к определению функции pk(t) при k>0. Разобьем период времени (0,t) на произвольное число n>k равных частей длины Относительно расположения поступления клиентов в этих частях возможны две гипотезы: H2 – хотя бы в одном из n промежутков поступит более одного
клиента. 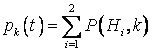 (11) (11)Двойная вероятность P(Hi,
k) включает вероятность
реализации гипотезы Hi и
одновременно вероятность того, что за период (0,t) поступает k
клиентов. Таким образом P(H1,
k) – вероятность того, что во
всех частях n периода (0,t) не
поступит более одного клиента, при этом общее количество клиентов за данный
период составит k. Следовательно, насчитывается k из n частей, которые
содержат по одному поступлению клиента, а в оставшихся (n – k) временных промежутках
клиенты не поступают. Чтобы определить вероятность
появления по одному клиенту в k из n промежутках времени, необходимо воспользоваться биномиальным
законом распределения: 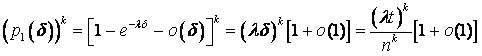 . (17) . (17)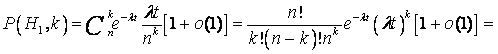 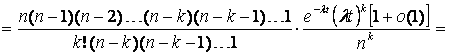 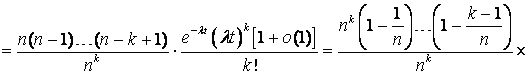 (18) (18)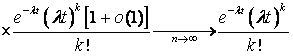 . .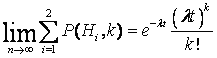 . (20) . (20)Так как pk(t) не
зависит от n, то, исходя из
равенства (11), получаем 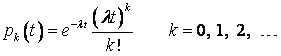 . (21) . (21)Вывод: для простейшего потока
число поступлений клиентов в промежутке времени длины t распределено по закону Пуассона с параметром
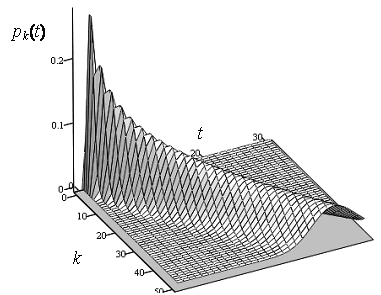 Различие двух простейших потоков
заключается только в разных значениях параметра Пусть w(t) – вероятность того, что за
промежуток времени t поступит по меньшей мере одна заявка: 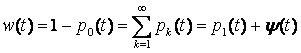 , (22) , (22)где 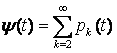 – вероятность поступления по меньшей мере двух заявок за промежуток времени t.
– вероятность поступления по меньшей мере двух заявок за промежуток времени t.Подобный предел существует у
любого стационарного потока и Из теории вероятности известно,
что математическое ожидание случайной величины, распределенной по
Пуассоновскому закону, равно параметру этого закона, и в нашем случае – 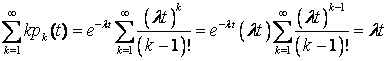 , (26) , (26) , (27) , (27)Определение 16. Математическое
ожидание числа заявок в единицу времени называется интенсивностью данного потока. Если поток не является
стационарным, то рассматривается вероятность  (29) (29)Пусть Вероятность того, что за
промежуток времени t подчиненного
распределению B(t), поступит k заявок, равна  . (30) . (30)
| |
| Категория: Имитационное моделирование | Добавил: kvn2us (10.02.2009) | | |
| Просмотров: 3958 |
