Парная регрессия

Пример регрессионного анализа

В R изначально включена таблица данных (women) о росте и весе 15 женщин в возрасте от 30 до 39 лет. Рост измеряется в дюймах, а вес – в фунтах. Узнаем, как зависит вес от роста.

Прежде всего используем lm() – модель линейной регрессии

> # Вычисление параметров уравнения регрессии
> lm.women<-lm(formula = weight ~ height, data = women)
> lm.women$coefficients
(Intercept)      height
  -87.51667     3.45000

> # Вывод модельных значений:
> a0 <- lm.women$coefficient[1]
> a1 <- lm.women$coefficient[2]
> xmin <- min(women$height)
> xmax <- max(women$height)
> x <- seq(from = xmin, to = xmax, length.out =100)
> y <- a0 + a1*x

> # Вывод графика зависимости:
> plot(women$height, women$weight, main="", xlab="Рост", ylab="Вес")
> grid()
> lines(x, y, col="red")

В итоге получим график, представленный на рис. 1.

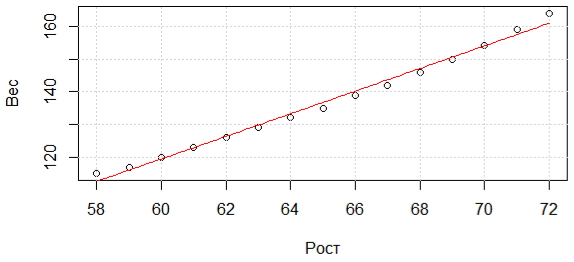
Рис. 1. Зависимость веса (y) от роста (x); y = –85.51 + 3.45 ∙ x

Чтобы посмотреть сведения о линейной аппроксимации используется функция summary()

> summary(lm.women)

Call:
lm(formula = weight ~ height, data = women)

Residuals:
    Min      1Q         Median        3Q       Max 
-1.7333   -1.1333   -0.3833    0.7417    3.1167 

Coefficients:
                 Estimate      Std. Error   t value     Pr(>|t|)
(Intercept) -87.51667       5.93694     -14.74    1.71e-09 ***
height        3.45000         0.09114      37.85    1.09e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared:  0.991,    Adjusted R-squared:  0.9903 
F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14
 

Итак, из раздела «Coefficient» отчета регрессионного анализа получаем такие коэффициенты, как:

a0 = -87.51667;

a1 = 3.45.

Тогда, уравнение регрессии имеет вид

y = -87.51667 + 3.45 ⋅ x

или

weight = -87.51667 + 3.45 * height

Модель содержит только один предиктор и, соответственно, при помощи F-критерия мы проверяем гипотезу об отсутствии связи между зависимой переменной и именно этим одним предиктором. F-критерий в этом примере составил 1433, что гораздо больше 1. Вероятность получить такое высокое значение при отсутствии связи между x и y очень мала (P = 1.091e-14). 

Чем меньше значение суммы квадратов остатков, т.е., чем ближе регрессионная линия ко всем наблюдениям одновременно, тем больше значение F-критерия будет отличаться от 1.

Также из отчета видим, что эти коэффициенты действительно являются значимыми и объясняют зависимость. Иными словами, нулевая гипотеза о том, что они стали лишь результатом погрешности, отвергается, а коэффициенты принимаются. Мы практически на 100%

(1 – 1.71e-09)*100%

уверены в том, что свободный член отличен от нуля.

Исходя из коэффициента детерминации R2, можем удостовериться, что регрессионная модель очень точно описывает данные. Более того с высокой степенью уверенности говорим об адекватности модели – зависимости предсказываемой величины от предикторов:

(1 – 1,091е-14)*100%. 

Эта интерпретация полностью применима для случая простой регрессии, когда модель включает лишь один предиктор. Однако при включении в модель нескольких независимых переменных, с такой интерпретацией следует быть очень осторожным, поскольку значение R2 всегда будет возрастать при увеличении числа предикторов в модели. Даже если некоторые из этих предикторов не имеют тесной связи с зависимой переменной, эта закономерность срабатывает – простой коэффициент детерминации будет отдавать предпочтение «переобученным» моделям. Поэтому рекомендуется применение скорректированного коэффициента детерминации (англ. adjusted R-squared):

R²_adj = R² − (1 − R²) * p/(n – p – 1),

где р – число параметров модели; n – объем выборки.

Чтобы в интерактивном режиме увидеть графики результатов анализа, вводим

> plot(lm.women)

Следует отметить, что прямую линию на график можно добавить с помощью abline().

Еще одно замечание связано с тем, что при потребности в исключении свободного члена регрессионной модели, в формулу добавляется -1.

lm(y ~ x – 1, data = …)

© Источники:

1. Шипунов А. Б., Балдин E. М., Волкова П. А., Коробейников А. И., Назарова С. А., Петров С. В., Суфиянов В. Г. (2014) Наглядная статистика. Используем R! – 296 с. URL: ashipunov.info
2. Доп. см. https://habrahabr.ru/post/195146/ - о функции summary().
3. r-analytics.blogspot.com

Регрессионный анализа. Часть 2 - сравнение регрессий >>>